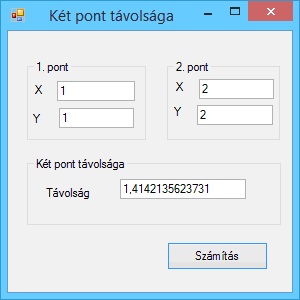
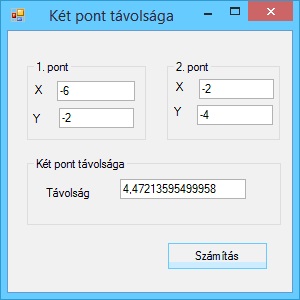
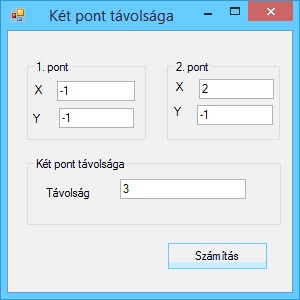
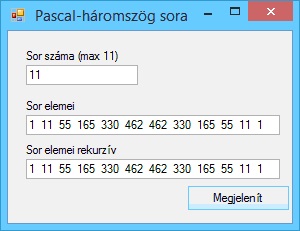
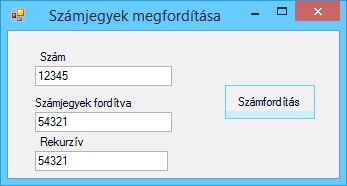
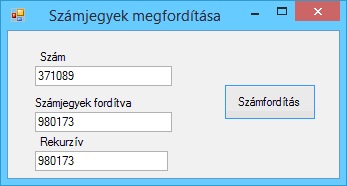
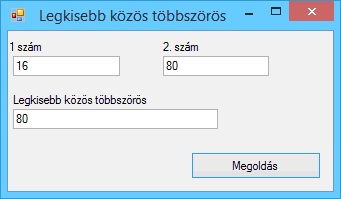
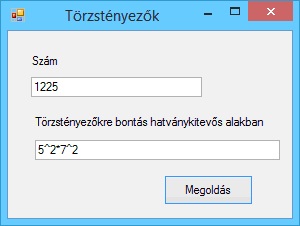
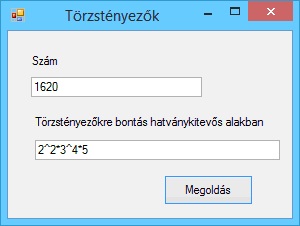
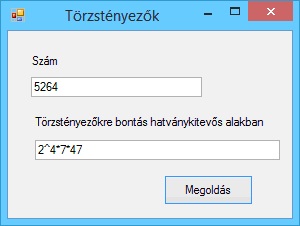
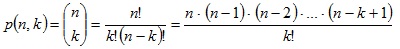Írjunk programot, amely kiszámítja két pont távolságát.

Két koordináta pont távolságát Pitagorasz tétellel számítjuk ki. A koordináták különbsége a derékszögű háromszög befogói, a távolság az átfogó számítása.

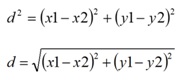
Négyzetgyökvonással kapjuk meg a távolságot:

Feladat megoldása:

         private void Számítás_Click(object sender, EventArgs e)
       {
          int p1x, p1y, p2x, p2y;
          double táv;
          if (textBox1.Text != "" && textBox2.Text != "" && 
              textBox3.Text != "" && textBox4.Text != "")
         {
             p1x = Int32.Parse(textBox1.Text);
             p1y = Int32.Parse(textBox2.Text);
             p2x = Int32.Parse(textBox3.Text);
             p2y = Int32.Parse(textBox4.Text);
             táv = Math.Sqrt(Math.Pow(p1x - p2x, 2) +
                             Math.Pow(p1y - p2y, 2));
             textBox5.Text = táv.ToString();
         }
       }

        private void textBox1_TextChanged(object sender, EventArgs e)
        {
            textBox5.Text = "";
        }

        private void textBox2_TextChanged(object sender, EventArgs e)
        {
            textBox5.Text = "";
        }

        private void textBox3_TextChanged(object sender, EventArgs e)
        {
             textBox5.Text = "";
        }

        private void textBox4_TextChanged(object sender, EventArgs e)
        {
             textBox5.Text = "";
        }

 A program futási eredményei:

 Írjunk programot, amely megjeleníti a Pascal-háromszög adott sorát. 

 A Pascal-háromszög első hat sorát jelenítjük meg.
Ha az elemek soron belüli indexe
      
akkor p(n,k) jelölje az n-edik sor, k. elemét. 
Például a 4-edik sor 3-adik eleme: p(4,3) = 6.

 Az elemek meghatározásának rekurzív algoritmusa:

ha k= 0 vagy k=n, akkor p(n,k) = 1, egyébként pedig p(n,k) = p(n-1,k-1) + p(n-1,k)

Például 5. sor 2. eleme:   p(5,2) = p(4,1) + p(4,2)

                                        p(5,2) =   1  +  4 =  5

 A nem rekurzív algoritmus valójában a binomiális együtthatók képlete:

 A feladat megoldása:

         // Rekurzív függvény
        static int rbinom(int n, int k)
        {
            if (k == 0 || k == n)
                 return 1;
            else
                 return rbinom(n - 1, k - 1) + rbinom(n - 1, k);
        }

        //Nem rekurzív függvény
        static int binom(int n, int k)
        {
            int g, b;
            b = 1;
            for (g = n - k + 1; g <= n; g++)
                b *=  g;
            for (g = 1; g <= k; g++)
                b /= g;
            return b; 
        }

        private void Megjelenít_Click(object sender, EventArgs e)
        {
            int sorszám, i;
            string sor= "";
            if (textBox1.Text != "")
            {
                sorszám = Int32.Parse(textBox1.Text);
                if (sorszám >= 0 && sorszám <= 11)
                {
                    for (i = 0; i <= sorszám; i++ )
                       sor += binom(sorszám,i).ToString() + "  ";
                    textBox2.Text = sor;
                    sor = "";
                    for (i = 0; i <= sorszám; i++)
                       sor += rbinom(sorszám, i).ToString() + "  ";
                    textBox3.Text = sor;
                }
                else
                    MessageBox.Show("Hibás adat", "Üzenet");
             }
        }

        private void textBox1_TextChanged(object sender, EventArgs e)
        {
            textBox2.Text = "";
            textBox3.Text = "";
        }

A program futási eredményei:

Írjunk programot, amely beolvas egy pozitív egész számot és a jegyeit fordítva írja vissza. A feladatot oldjuk meg kétféle módon.

A feladat megoldása:

       // Rekurzív megoldás
        static string Számfordít(int sz, string s)
        {
            s = (sz % 10).ToString();  
            sz /= 10;
            if (sz != 0)
                return s + Számfordít(sz,s);  
            else
                return s;
            }

         private void Számfordítás_Click(object sender, EventArgs e)
         {
            int szám;
            string s1 = "", s2= "";
            if (textBox1.Text != "")
            {
                szám = Int32.Parse(textBox1.Text);
                if (szám > 0)
                {
                    s1 = Számfordít(szám, s1);
                    textBox3.Text = s1;
                    while (szám != 0)
                    {
                        s2 += szám % 10;
                        szám /= 10;
                    }
                    textBox2.Text = s2;
                }
                else
                {
                    MessageBox.Show("Hibás adat!", "Üzenet");
                    textBox1.Text = "";
                }
            }
        }

        private void textBox1_TextChanged(object sender, EventArgs e)
        {
             textBox2.Text = ""; textBox3.Text = "";
        }

A program futási eredményei:

Írjunk programot, amely két egész szám legkisebb közös többszörösét keresi meg.

A feladatot do-while ciklussal oldjuk meg.

A feladat megoldása:

        // A legkisebb közös többszörös keresése
        private void button1_Click(object sender, EventArgs e)
        {
            int szám1, szám2, osztó1, osztó2, lktöbb = 0, sz;
            if (textBox1.Text != "" && textBox2.Text != "")
            {
                szám1 = Int32.Parse(textBox1.Text);
                szám2 = Int32.Parse(textBox2.Text);
                if (szám1 > szám2) // szám2 legyen a nagyobb
                {
                    sz = szám2; szám2 = szám1;
                    szám1 = sz;
                }
                if (szám1 > 1 && szám2 > 1)
                {
                    lktöbb = 1;
                    do
                    {
                        do
                        {   
                            osztó1 = 2;
                            while (szám1 % osztó1 != 0)
                                osztó1++;
                            if (szám2 % szám1 == 0) szám2 /= osztó1;
                            lktöbb *= osztó1; szám1 /= osztó1;
                        } while (szám1 != 1);
                        do
                        {
                            osztó2 = 2;
                            while (szám2 % osztó2 != 0)
                                 osztó2++;
                            lktöbb *= osztó2; szám2 /= osztó2;
                        } while (szám2 != 1);
                    } while (szám1 != 1 && szám2 != 1);
                }
                 else
                      MessageBox.Show("Az adat hibás!", "Üzenet");
                 textBox3.Text = "" + lktöbb;
           }

        } 

        private void textBox1_TextChanged(object sender, EventArgs e)
        {
             textBox3.Text = "";
        }

        private void textBox2_TextChanged(object sender, EventArgs e)
        {
             textBox3.Text = "";
        }

A program futási eredményei:

Írjunk programot, amely két egész számnak megkeresi a legkisebb közös többszörö­sü­ket.

Algoritmus készítése

Keressük meg 8 és 18 egész számok legkisebb közös többszörösét kézi szá­mo­lással.

 
A legkisebb közös többszörös meghatározásához törzstényezőkre bontjuk a számokat. Először a szám1-nek keressük a törzstényezőit, és a megtalált törzs­té­nyezővel el­osztjuk a szám1-t. A szám2-őt csak akkor osztjuk a törzstényező­vel, ha az osztója a számnak. A legkisebb többszöröst beszorozzuk a megtalált törzstényezővel, ezt addig végezzük, míg a szám1 1 lesz. Ezután a szam2-vel is addig folytatjuk a törzstényezőre bontást míg a szám2 is 1-gyé válik.

 A feladat megoldása:

            // Legkisebb közös többszörös
        private void button1_Click(object sender, EventArgs e)
        {
             int szám1, szám2, osztó1, osztó2, lktöbb= 0, sz;
             if (textBox1.Text != "" && textBox2.Text != "")
             {
                 szám1 = Int32.Parse(textBox1.Text);
                 szám2 = Int32.Parse(textBox2.Text);
                 if (szám1 > szám2)
                 {
                     sz = szám2; szám2 = szám1;
                     szám1 = sz;
                 }
                 if (szám1 > 1 && szám2 > 1)
                 {
                     lktöbb = 1;
                     while (szám1 != 1)
                     {
                         osztó1 = 2;
                         while (szám1 % osztó1 != 0)
                              osztó1++;
                         if (szám2 % szám1 == 0)
                              szám2 /= osztó1;
                         lktöbb *= osztó1;
                         szám1 /= osztó1;
                     }
                     while (szám2 != 1)
                     {
                         osztó2 = 2;
                         while (szám2 % osztó2 != 0)
                              osztó2++;
                         szám2 /= osztó2;
                         lktöbb *= osztó2;
                    }
                 }
                 else
                      MessageBox.Show("Az adat hibás!", "Üzenet");
                 textBox3.Text = "" + lktöbb;
             }
         }

        // Ha az első adat változik, a korábbi eredmény törlődik
        private void textBox1_TextChanged(object sender, EventArgs e)
        {

             textBox3.Text = "";
        }

        // Ha a második adat változik, a korábbi eredmény törlődik
        private void textBox2_TextChanged(object sender, EventArgs e)
        {
             textBox3.Text = "";
        }

 A program futási eredményei:

Írjunk programot, amely euklideszi algoritmus segítségével megkeresi két pozitív egész szám leg­nagyobb közös osztóját!

Az euklideszi algoritmus szerint, ha a kisebbik szám maradék nélkül megvan a nagyobbikban, akkor a kisebbik lesz a legnagyobb közös osztó. Ha van maradék, a legnagyobb közös osztó kisebb vagy egyenlő lesz a maradékkal. A következő próbálkozásnál a kisebbik szám lép az osztandó, a maradék pedig az osztó he­lyébe. Az algoritmus így mindaddig folytatódik, míg a maradék nulla nem lesz, ekkor az aktuális osztó lesz a legnagyobb közös osztó.

A feladat megoldása:

           // Legnagyobb közös osztó Euklideszi algoritmussal
        private void button1_Click(object sender, EventArgs e)
        {
            int szám1, szám2, osztó = 0, r;
            if (textBox1.Text != "" && textBox2.Text != "")
            {
                szám1 = Int32.Parse(textBox1.Text);
                szám2 = Int32.Parse(textBox2.Text);
                if (szám1 > 0 && szám2 > 0)
                {
                    do
                    {
                        r = szám1 % szám2;
                        if (r == 0)
                             osztó = szám2;
                        else
                        {
                            szám1 = szám2;
                            szám2 = r;
                        }
                    } while (r > 0 );
                    if (osztó == 1)
                         textBox3.Text =
                             "Nincs legnagyobb közös osztójuk.";
                    else
                         textBox3.Text = "" + osztó;
                 }
             }
         }

        // Ha az első adat változik, a korábbi eredmény törlődik
        private void textBox1_TextChanged(object sender, EventArgs e)
        {
             textBox3.Text = "";
        }

        // Ha a második adat változik, a korábbi eredmény törlődik
        private void textBox2_TextChanged(object sender, EventArgs e)
        {
             textBox3.Text = "";
        }

A program futási eredményei:

1. megoldás  while ciklussal

Algoritmus készítés

 Az algoritmushoz készítsünk kézi számolást! Határozzuk meg 16 és 40 legna­gyobb közös osztóját. A két szám közül kiválasztjuk a kisebbet, majd 2-től egyesével növelve a kisebb szám-ig a két szám közös osz­tóit meghatározzuk. 

16      osztói:       2     4             8     16
40      osztói:       2     4     5      8
közös osztók     2     4             8

 Tehát a 16 és 40 egész számoknak 8 a legnagyobb közös osztója.

 A program megtervezése:

• A program megírásához szükségünk lesz négy változóra:

            szám1,szám2   tárolja a két számot, melynek a legnagyobb
                                     közös  osztóját keressük,

            osztó                tartalmazza az aktuális osztót,

            közös               az aktuális közös osztó tárolására szolgál.

• A szám1 és szám2 változókba beolvassuk a két egész számot.
• Az osztó kezdőértéke 2, innen indul az oszthatóság vizsgálat.
• A közös változó kezdőértéke 0, ha értéke nullánál nagyobb lesz,
  azt je­lenti, hogy a két számnak van közös osztója, az utoljára
  felvett érték lesz a legna­gyobb közös osztó.

        A while ciklus addig működik, míg az osztó kisebb a kisebbik számnál, 
        legyen az akár a szám1 vagy a szám2.

           (osztó <= szám1 && osztó <= szám2)       

• A ciklus magja megvizsgálja, hogy az osztó mindkettő osztója-e:

           (szám1 % osztó = 0 && szám2 % osztó = 0)     

        Ha a feltétel teljesül, akkor a közös változó felveszi az osztó értékét

• Gondoskodni kell a ciklusban az osztó változó növeléséről:

          osztó++;

• A ciklus működésének befejezése után a közös változó tartalma dönti el,
  hogy találtunk legnagyobb közös osztót (közös>0), vagy nem (közös==0).

A feladat megoldása:

                    // Legnagyobb közös osztó keresése
        private void button1_Click(object sender, EventArgs e)
        {
            int szám1, szám2, osztó, közös= 0;
            if (textBox1.Text != "" && textBox2.Text != "")
            {
                szám1 = Int32.Parse(textBox1.Text);
                szám2 = Int32.Parse(textBox2.Text);
                osztó = 2;
                közös = 0;
                while (osztó <= szám1 && osztó <= szám2)
                {
                    if(szám1 % osztó == 0 && szám2 % osztó == 0)
                        közös = osztó;
                    osztó++;
                }
                if (közös == 0)
                    textBox3.Text =
                        "Nincs legnagyobb közös osztójuk.";
                else
                    textBox3.Text = "" + közös;
            }
        }

        // Ha az első adat változik a korábbi eredmény törlődik
        private void textBox1_TextChanged(object sender, EventArgs e)
        {
             textBox3.Text = "";
        }

        // Ha a második adat változik a korábbi eredmény törlődik
        private void textBox2_TextChanged(object sender, EventArgs e)
        {
             textBox3.Text = "";
        }

A program futási eredményei:

A legnagyobb közös osztó keresését do-while ciklussal is megoldhatjuk. Az 1. megoldás programot felhasználva az alábbi módosításokat kell végrehaj­tanunk:

• Mivel a do-while ciklus hátul tesztelő, ezért a számok beolvasása után egy feltételes utasításban meg kell vizsgálnunk, hogy a szám1 és a szám2 tar­talma nagyobb-e 1-nél, mert csak akkor foglalkozunk a legnagyobb kö­zös osztó keresésével.
• A ciklusmag változatlan marad, a leállási feltétel:

       (osztó <= szám1 && osztó <= szám2)

a do-while ciklus addig működik, míg a feltétel igaz, tehát az osztó egyik számot sem haladta túl. 

 A feladat megoldása:

            // Legnagyobb közös osztó megoldása do-while ciklussal
         private void button1_Click(object sender, EventArgs e)
         {
            int szám1, szám2, osztó, közös = 0;
            if (textBox1.Text != "" && textBox2.Text != "")
            {
                szám1 = Int32.Parse(textBox1.Text);
                szám2 = Int32.Parse(textBox2.Text);
                osztó = 2;
                közös = 0;
                if (szám1 > 1 && szám2 > 1)
                {
                    do
                    {
                        if (szám1 % osztó == 0 && szám2 % osztó == 0)
                            közös = osztó;
                        osztó++;
                    } while (osztó <= szám1 && osztó <= szám2);
                }
                if (közös == 0)
                     textBox3.Text =
                        "Nincs legnagyobb közös osztójuk.";
                else
                     textBox3.Text = "" + közös;
             }
         }

       // Ha az első adat változik, a korább eredmény törlődik
       private void textBox1_TextChanged(object sender, EventArgs e)
       {
            textBox3.Text = "";
       }

       // Ha a második adat változik, a korább eredmény törlődik
       private void textBox2_TextChanged(object sender, EventArgs e)
       {
            textBox3.Text = "";
       }

 A program futási eredményei:

Írjunk programot, amely egy egész számot törzstényezős és hatványkitevős alakra bontja függvénnyel.

A feladat megoldása:

             static void Törzstényezős(int szám, out string s)
         {
            int osztó, db = 0;
            s = "";
            while (szám != 1)
            {
                osztó = 2;
                while (szám % osztó != 0)
                {
                    osztó++;
                }
                szám = szám / osztó;
                db++;
                if (szám == 1) s += osztó;
                else s += osztó + "*";
            }
        }

        static void Hatványkitevős(int szám, out string s)
        {
            int osztó, előzö, hatv;
            bool első = true;
            s = "";
            előzö = 2; hatv = 0;
            while (szám != 1)
            {
                osztó = 2;
                while (szám % osztó != 0)
                {
                    osztó++;
                }
                if (első)
                {
                    előzö = osztó;
                    s += osztó;
                    első = false;
                }
                if (előzö == osztó) hatv++;
                else
                {
                    if (hatv > 1)
                    {
                        s += "^" + hatv + "*" + osztó;
                        hatv = 1;
                    }
                    else
                        s += "*" + osztó;
                }
                szám = szám / osztó;
                if (szám == 1 && előzö == osztó && hatv > 1)
                    s += "^" + hatv;
                előzö = osztó;
            }
        }

        private void Megoldás_Click(object sender, EventArgs e)
        {
            int szám;
            string s1, s2;
            if(textBox1.Text != "")
            {
                szám = Int32.Parse(textBox1.Text);
                if (szám > 0)
                {
                    Törzstényezős(szám, out s1);
                    textBox2.Text = s1;
                    Hatványkitevős(szám, out s2);
                    textBox3.Text = s2;
                }
                else
                    MessageBox.Show("Az adat nem megfelelő");
            }
        }

        private void textBox1_TextChanged(object sender, EventArgs e)
        {
            textBox2.Text = "";
            textBox3.Text = "";
        }

A program futási eredményei:

Írjunk programot, amely egy egész szám  törzstényezős alakjánál tömörebb, hatványkitevős alakban jelenítse meg az eredményt.

A törzstényezős alak kiíratásánál használható a tömörebb hatványkitevős alak:

       64  =  2*2*2*2*2*2 = 2^6

       576 =  2*2*2*2*2*2*3*3 = 2^6*3^2

A feladat megoldása:

                     // Törzstényezők kiírása hatványkitevős alakban
         private void button1_Click(object sender, EventArgs e)
         {
            int szám, osztó, előzö, hatv;
            bool első = true;
            string s = "";
            if (textBox1.Text != "")
            {
                szám = Int32.Parse(textBox1.Text);
                if (szám > 0)
                {
                    előzö = 2; hatv = 0;
                    while (szám != 1)
                    {
                        osztó = 2;
                        while (szám % osztó != 0)
                        {
                            osztó++;
                        }
                        if (első)
                        {
                            előzö = osztó;
                            s += osztó;
                            első = false;
                        }
                        if (előzö == osztó)
                              hatv++; // azonos osztó esetén
                                      // növeljük  hatv értékét
                        else
                        {
                            if (hatv > 1)
                            {
                                // hatv kiírásra kerül és
                                // az osztó is
                                s += "^" + hatv + "*" + osztó;
                                hatv = 1; // újra 1 hatv értéke
                            }
                            else
                                s += "*" + osztó; // új osztó kiírása
                        }
                        szám = szám / osztó;
                        if (szám == 1 && előzö == osztó && hatv > 1 )
                           s += "^" + hatv; // utolsó kiírás
                        előzö = osztó; // előzö beállítása
                    }
                    textBox2.Text = s;
                }
                else
                    MessageBox.Show("Hibás adat!", "Üzenet");
            }
        }

        // Ha az adat változik a korábbi eredmény törlődik
        private void textBox1_TextChanged(object sender, EventArgs e)
        {
             textBox2.Text = "";
        }

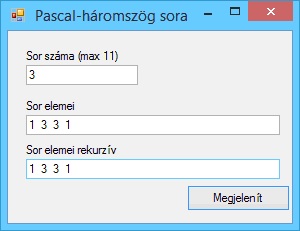
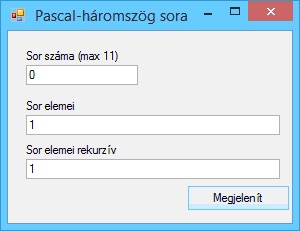
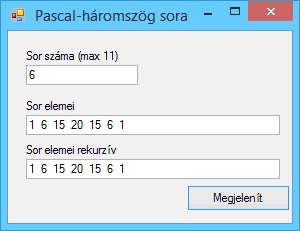
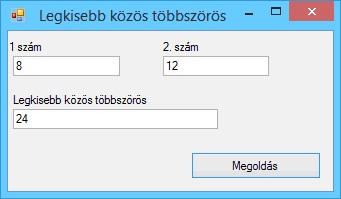
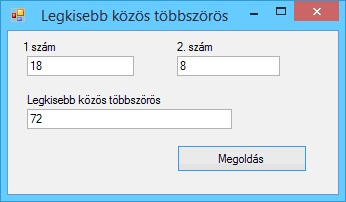
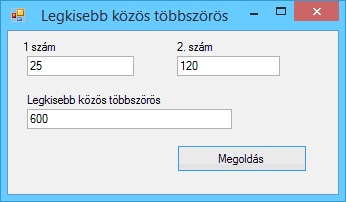
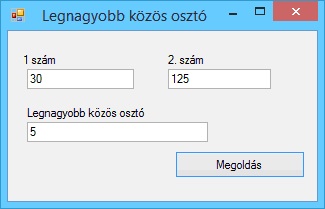
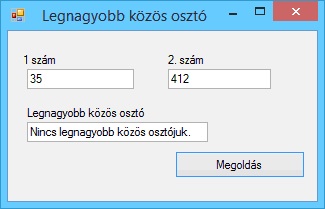
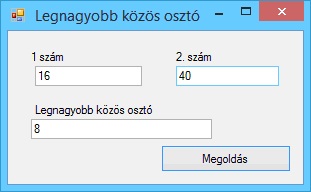
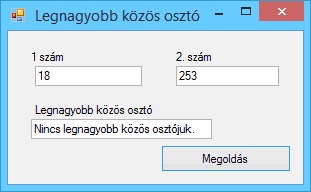
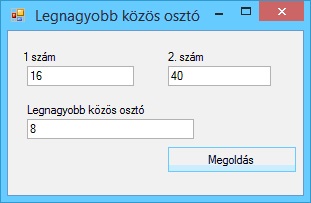
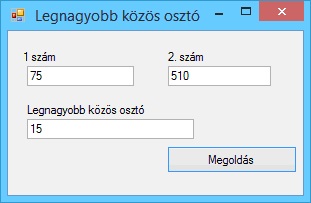
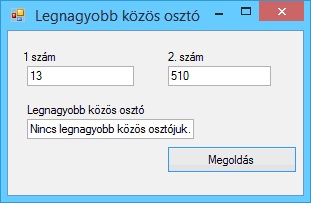
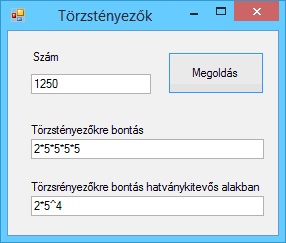
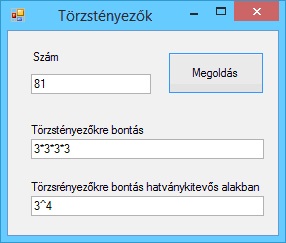
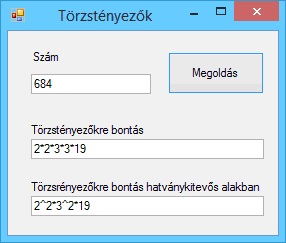
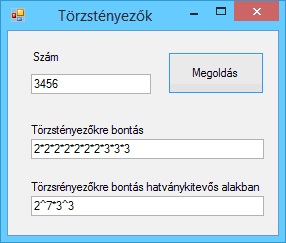
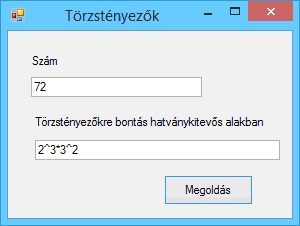
A program futási eredményei: