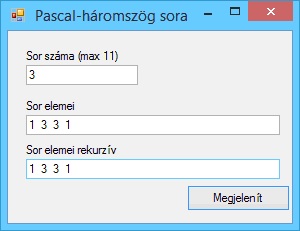
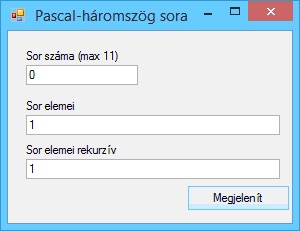
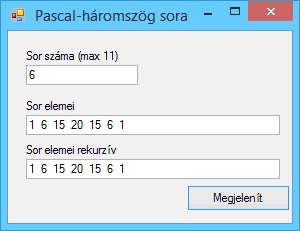
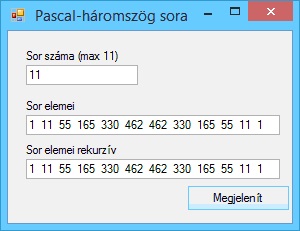
Írjunk programot, amely megjeleníti a Pascal-háromszög adott sorát.
A Pascal-háromszög első hat sorát jelenítjük meg.
Ha az elemek soron belüli indexe
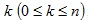
akkor p(n,k) jelölje az n-edik sor, k. elemét.
Például a 4-edik sor 3-adik eleme: p(4,3) = 6.

Az elemek meghatározásának rekurzív algoritmusa:
ha k= 0 vagy k=n, akkor p(n,k) = 1, egyébként pedig p(n,k) = p(n-1,k-1) + p(n-1,k)
Például 5. sor 2. eleme: p(5,2) = p(4,1) + p(4,2)
p(5,2) = 1 + 4 = 5
A nem rekurzív algoritmus valójában a binomiális együtthatók képlete:
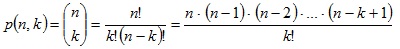
A feladat megoldása:
// Rekurzív függvény
static int rbinom(int n, int k)
{
if (k == 0 || k == n)
return 1;
else
return rbinom(n - 1, k - 1) + rbinom(n - 1, k);
}
//Nem rekurzív függvény
static int binom(int n, int k)
{
int g, b;
b = 1;
for (g = n - k + 1; g <= n; g++)
b *= g;
for (g = 1; g <= k; g++)
b /= g;
return b;
}
private void Megjelenít_Click(object sender, EventArgs e)
{
int sorszám, i;
string sor= "";
if (textBox1.Text != "")
{
sorszám = Int32.Parse(textBox1.Text);
if (sorszám >= 0 && sorszám <= 11)
{
for (i = 0; i <= sorszám; i++ )
sor += binom(sorszám,i).ToString() + " ";
textBox2.Text = sor;
sor = "";
for (i = 0; i <= sorszám; i++)
sor += rbinom(sorszám, i).ToString() + " ";
textBox3.Text = sor;
}
else
MessageBox.Show("Hibás adat", "Üzenet");
}
}
private void textBox1_TextChanged(object sender, EventArgs e)
{
textBox2.Text = "";
textBox3.Text = "";
}
A program futási eredményei: