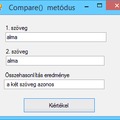
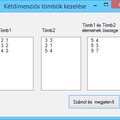
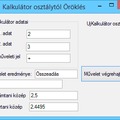
Írjunk programot, amely a megadott sorig megjeleníti a Pascal-háromszög sorait.
A Pascal-háromszög első hat sorát jelenítjük meg.
Ha az elemek soron belüli indexe
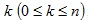
akkor p(n,k) jelölje az n-edik sor, k. elemét.
Például a 4-edik sor 3-adik eleme: p(4,3) = 6.

Az elemek meghatározásának rekurzív algoritmusa:
ha k= 0 vagy k=n, akkor p(n,k) = 1, egyébként pedig p(n,k) = p(n-1,k-1) + p(n-1,k)
Például 5. sor 2. eleme: p(5,2) = p(4,1) + p(4,2)
p(5,2) = 1 + 4 = 5
A nem rekurzív algoritmus valójában a binomiális együtthatók képlete:
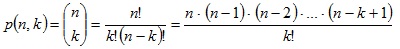
A feladat megoldása:
private void Létrehoz_Click(object sender, EventArgs e)
{
if (textBox2.Text != "")
{
int sorokSzáma = Convert.ToInt32(textBox2.Text);
int mezőSzélesség = (int)(6 * Math.Log(sorokSzáma));
long binomEgyüttható = 0;
string szövegsor;
textBox1.Text = "";
// soronként állítjuk elő a Pascal háromszöget
for (int sor = 1; sor <= sorokSzáma; sor++)
{
// bevezető szóközök
szövegsor = new string(' ', mezőSzélesség *
sorokSzáma - sor) / 2);
// az aktuális sorban a binomiális
// együtthatók számítása
binomEgyüttható = 1;
for (int oszlop = 0; oszlop < sor; oszlop++)
{
if (oszlop > 0)
{
binomEgyüttható = binomEgyüttható *
(sor - oszlop) / oszlop;
}
szövegsor += string.Format("{0," +
mezőSzélesség + "}",
binomEgyüttható);
}
textBox1.Text += szövegsor + "\r\n";
}
}
}
private void textBox2_TextChanged(object sender, EventArgs e)
{
textBox1.Text = "";
}
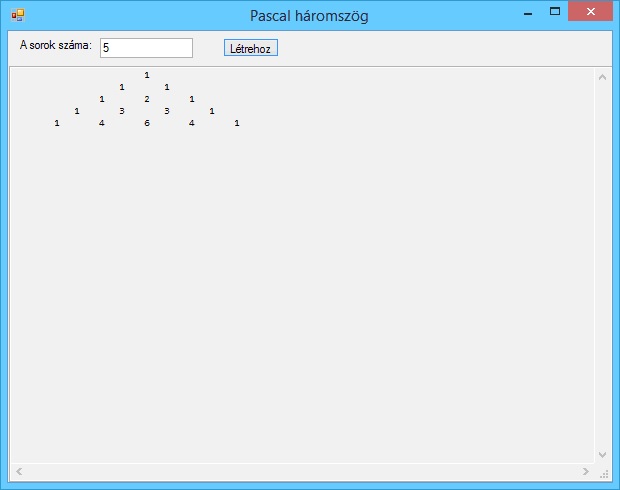
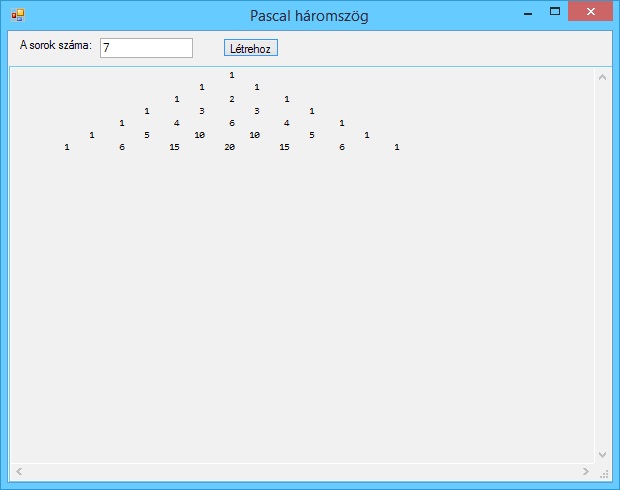
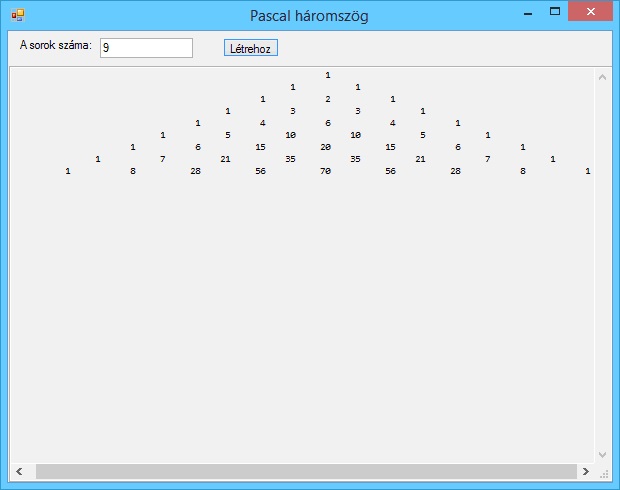
A program futási eredményei: