Készítsünk olyan bűvös négyzetet, amely 3,5,7 max. 9 méretű mátrix lehet. A bűvös négyzet lényege, hogy a négyzetben lévő számok sorainak és oszlopainak valamint átlóinak összege mindig azonos.
A feladat megoldása:
int max = 9; // a mátrix max méret
static int Agrippa(int n, ref int[] mátrix)
{
int i, j, IVAL; // pozíció és a beírandó szám
for (i = 0; i < n * n; i++)
mátrix[i] = 0; // mátrix nullázása
// kezdőértékek beállítása
j = (n + 1) / 2; i = j + 1; IVAL = 1;
while (mátrix[i + n * j] >= 0) //ha < 0, akkor vége
{
if (mátrix[i + n * j] == 0)
{
mátrix[i + n * j] = IVAL;
if (IVAL == n * n) return 1; // sikeres
IVAL++; i++; j++; // lépés le jobbra
if (i > n) // ha kint vagyunk a négyzetből
{
if (j > n)
{ i = 2; j = n; }
else i = 1;
}
else
{
if (j > n) j = 1;
}
}
else // már van ott szám
{
i++; j--;
if (i > n) i = 1;
}
}
return 0; // hiba;
}
private void Generálás_Click(object sender, EventArgs e)
{
int i, j, n, jel;
int[] mtömb;
if (textBox1.Text != "")
{
n = Int32.Parse(textBox1.Text);
if (n < 3 || n > max || ((n % 2) == 0))
{
MessageBox.Show(
"A méret: 3,5,7,9 lehet, nem lehet páros szám!",
"Üzenet");
textBox1.Text = "";
}
else
{
mtömb = new int[(max + 1) * (max + 1)];
jel = Agrippa(n, ref mtömb);
if (jel == 0)
MessageBox.Show("Futási hiba", "Üzenet");
else
{
textBox2.Text = "";
MessageBox.Show("Sikeres futás", "Üzenet");
for (i = 1; i <= n; i++) // sorok
{
for (j = 1; j <= n; j++)
{
textBox2.Text +=
mtömb[i + j * n].ToString()
+ " ";
}
richTextBox1.Text += textBox2.Text
+ "\n";
textBox2.Text = "";
}
}
}
}
}
private void textBox1_TextChanged(object sender, EventArgs e)
{
richTextBox1.Text = "";
}
A program futási eredményei:
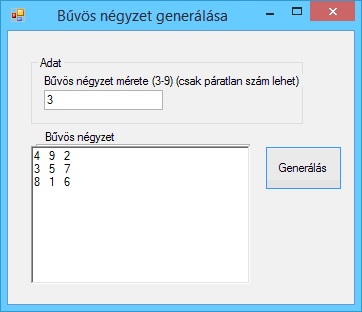
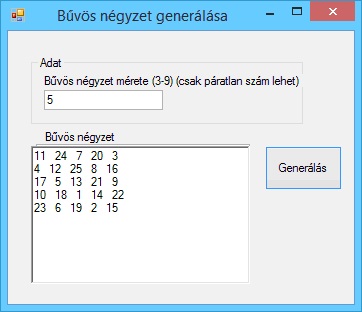
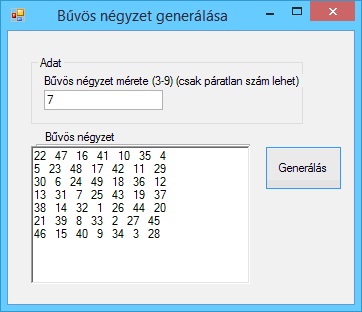
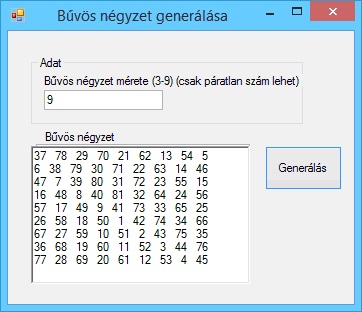
Hibajelzés: